【作业向】程序设计思维与实践 Week13作业
♔A TT的神秘任务 - 必做
♔Problem
这一天,TT 遇到了一个神秘人。
神秘人给了两个数字,分别表示 n 和 k,并要求 TT 给出 k 个奇偶性相同的正整数,使得其和等于 n。
例如 n = 10,k = 3,答案可以为 [4 2 4]。
TT 觉得这个任务太简单了,不愿意做,你能帮他完成吗?
本题是SPJ
♔Input
第一行一个整数 T,表示数据组数,不超过 1000。
之后 T 行,每一行给出两个正整数,分别表示 n(1 ≤ n ≤ 1e9)、k(1 ≤ k ≤ 100)。
♔Output
如果存在这样 k 个数字,则第一行输出 “YES”,第二行输出 k 个数字。
如果不存在,则输出 “NO”。
♔Example
♔Input
1 | 8 |
♔Output
1 | YES |
♔解题思路
本题可以使用贪心的方法,检查用k-1个1填充后剩下的数字是否是奇数,或用k-1个2填充后剩下的数是否是偶数即可判断。
♔代码
1 |
|
♔B TT的神秘任务 - 必做
♔Problem
在你们的帮助下,TT 轻松地完成了上一个神秘任务。
但是令人没有想到的是,几天后,TT 再次遇到了那个神秘人。
而这一次,神秘人决定加大难度,并许诺 TT,如果能够完成便给他一个奖励。
任务依旧只给了两个数字,分别表示 n 和 k,不过这一次是要求 TT 给出无法被 n 整除的第 k 大的正整数。
例如 n = 3,k = 7,则前 7 个无法被 n 整除的正整数为 [1 2 4 5 7 8 10],答案为 10。
好奇的 TT 想要知道奖励究竟是什么,你能帮帮他吗?
♔Input
第一行一个整数 T,表示数据组数,不超过 1000。
之后 T 行,每一行给出两个正整数,分别表示 n(2 ≤ n ≤ 1e9)、k(1 ≤ k ≤ 1e9)。
♔Output
对于每一组数据,输出无法被 n 整除的第 k 大的正整数。
♔Example
♔Input
1 | 6 |
♔Output
1 | 10 |
♔解题思路
我们知道,1~k中可以被n整除的数有k/n个,因此答案需要k+k/n,但新加的k/n个数中还会有被n整除的数(禁止套娃),因此我们需要进行循环操作,直到ans/n-k/n等于0。
♔代码
1 |
|
♔C TT的奖励 - 必做
♔Problem
在大家不辞辛劳的帮助下,TT 顺利地完成了所有的神秘任务。
神秘人很高兴,决定给 TT 一个奖励,即白日做梦之捡猫咪游戏。
捡猫咪游戏是这样的,猫咪从天上往下掉,且只会掉在 [0, 10] 范围内,具体的坐标范围如下图所示。

TT 初始站在位置五上,且每秒只能在移动不超过一米的范围内接住掉落的猫咪,如果没有接住,猫咪就会跑掉。例如,在刚开始的一秒内,TT 只能接到四、五、六这三个位置其中一个位置的猫咪。
喜爱猫咪的 TT 想要接住尽可能多的猫咪,你能帮帮他吗?
♔Input
多组样例。每组样例输入一个 m (0 < m < 100000),表示有 m 只猫咪。
在接下来的 m 行中,每行有两个整数 a b (0 < b < 100000),表示在第 b 秒的时候有一只猫咪掉落在 a 点上。
注意,同一个点上同一秒可能掉落多只猫咪。m = 0 时输入结束。
♔Output
输出一个整数 x,表示 TT 可能接住的最多的猫咪数。
♔Examples
♔Input
1 | 6 |
♔Output
1 | 4 |
♔解题思路
类似于dp入门题目中的数字三角形
用dp[i] [j]代表在i位置的第j秒的接住猫咪数,从后向前遍历,状态转移方程为
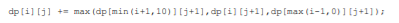
♔代码
1 |
|
♔D TT的苹果树 - 选做
♔Problem
在大家的三连助攻下,TT 一举获得了超级多的猫咪,因此决定开一间猫咖,将快乐与大家一同分享。并且在开业的那一天,为了纪念这个日子,TT 在猫咖门口种了一棵苹果树。
一年后,苹果熟了,到了该摘苹果的日子了。
已知树上共有 N 个节点,每个节点对应一个快乐值为 w[i] 的苹果,为了可持续发展,TT 要求摘了某个苹果后,不能摘它父节点处的苹果。
TT 想要令快乐值总和尽可能地大,你们能帮帮他吗?
♔Input
结点按 1~N 编号。
第一行为 N (1 ≤ N ≤ 6000) ,代表结点个数。
接下来 N 行分别代表每个结点上苹果的快乐值 w[i](-128 ≤ w[i] ≤ 127)。
接下来 N-1 行,每行两个数 L K,代表 K 是 L 的一个父节点。
输入有多组,以 0 0 结束。
♔Output
每组数据输出一个整数,代表所选苹果快乐值总和的最大值。
♔Examples
♔Input
1 | 7 |
♔Output
1 | 5 |
♔解题思路
这一题是一个树形dp,类似于比较经典的树形dp题目没有上司的舞会
设状态f[i] [0]为以i为根且未选择i节点的最大苹果数,f[i] [1]为以i为根且选择了i节点的最大苹果数。转移方程为
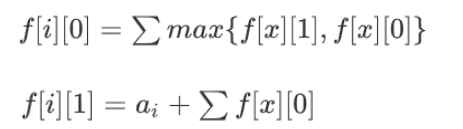
其中,x为i的子节点,ai为节点i的苹果数。
然后用dfs的方法从根节点开始遍历这棵树即可。
♔代码
1 |
|
♔E TT的神秘任务3 - 选做
♔Problem
TT 猫咖的生意越来越红火,人越来越多,也越来越拥挤。
为了解决这个问题,TT 决定扩大营业规模,但猫从哪里来呢?
TT 第一时间想到了神秘人,想要再次通过完成任务的方式获得猫咪。
而这一次,神秘人决定加大难度。
给定一个环,A[1], A[2], A[3], … , A[n],其中 A[1] 的左边是 A[n]。要求从环上找出一段长度不超过 K 的连续序列,使其和最大。
这一次,TT 陷入了沉思,他需要你们的帮助。
♔Input
第一行一个整数 T,表示数据组数,不超过 100。
每组数据第一行给定两个整数 N K。(1 ≤ N ≤ 100000, 1 ≤ K ≤ N)
接下来一行,给出 N 个整数。(-1000 ≤ A[i] ≤ 1000)。
♔Output
对于每一组数据,输出满足条件的最大连续和以及起始位置和终止位置。
如果有多个结果,输出起始位置最小的,如果还是有多组结果,输出长度最短的。
♔Examples
♔Input
1 | 4 |
♔Output
1 | 7 1 3 |
♔解题思路
本题用到了单调队列优化的dp,同时因为是一个环,因此我们将环进行复制,以达到展开的目的。
具体的解题方法为:
先求出a数组的前缀和(展开后的),然后将a数组的第1~n个加入到单调队列中(表示结尾),然后开始枚举开头,对于每一个开头i,先将a的第i+n-1个加入到单调队列,然后将单调队列中在a中下标小于i的头节点弹出。然后进行求解,更新最大值即数组的开头结尾即可。
同时,因为要起始位置最小以及长度最短的,起始位置最小可以用小于号更新答案来保证,长度最短可以用单调队列,在排序的时候将在a中的下标作为第二关键字来排序保证。
♔代码
1 |
|
