【作业向】程序设计思维与实践 Week9 作业

发表于 | 分类于 ，
字数统计: 4.8k | 阅读时长 ≈ 23

【作业向】程序设计思维与实践 Week9作业

♔A 咕咕东的目录管理器

♔Problem

咕咕东的雪梨电脑的操作系统在上个月受到宇宙射线的影响，时不时发生故障，他受不了了，想要写一个高效易用零bug的操作系统 —— 这工程量太大了，所以他定了一个小目标，从实现一个目录管理器开始。前些日子，东东的电脑终于因为过度收到宇宙射线的影响而宕机，无法写代码。他的好友TT正忙着在B站看猫片，另一位好友瑞神正忙着打守望先锋。现在只有你能帮助东东！

初始时，咕咕东的硬盘是空的，命令行的当前目录为根目录 root。

目录管理器可以理解为要维护一棵有根树结构，每个目录的儿子必须保持字典序。

img

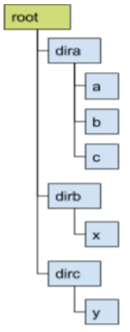
现在咕咕东可以在命令行下执行以下表格中描述的命令：

命令 类型 实现 说明
MKDIR s 操作 在当前目录下创建一个子目录 s，s 是一个字符串 创建成功输出 “OK”；若当前目录下已有该子目录则输出 “ERR”
RM s 操作 在当前目录下删除子目录 s，s 是一个字符串 删除成功输出 “OK”；若当前目录下该子目录不存在则输出 “ERR”
CD s 操作 进入一个子目录 s，s 是一个字符串（执行后，当前目录可能会改变） 进入成功输出 “OK”；若当前目录下该子目录不存在则输出 “ERR” 特殊地，若 s 等于 “…” 则表示返回上级目录，同理，返回成功输出 “OK”，返回失败（当前目录已是根目录没有上级目录）则输出 “ERR”
SZ 询问 输出当前目录的大小 也即输出 1+当前目录的子目录数
LS 询问 输出多行表示当前目录的 “直接子目录” 名 若没有子目录，则输出 “EMPTY”；若子目录数属于 [1,10] 则全部输出；若子目录数大于 10，则输出前 5 个，再输出一行 “…”，输出后 5 个。
TREE 询问 输出多行表示以当前目录为根的子树的前序遍历结果 若没有后代目录，则输出 “EMPTY”；若后代目录数+1（当前目录）属于 [1,10] 则全部输出；若后代目录数+1（当前目录）大于 10，则输出前 5 个，再输出一行 “…”，输出后 5 个。若目录结构如上图，当前目录为 “root” 执行结果如下，img
UNDO 特殊 撤销操作 撤销最近一个 “成功执行” 的操作（即MKDIR或RM或CD）的影响，撤销成功输出 “OK” 失败或者没有操作用于撤销则输出 “ERR”

♔Input

输入文件包含多组测试数据，第一行输入一个整数表示测试数据的组数 T （T <= 20）；

每组测试数据的第一行输入一个整数表示该组测试数据的命令总数 Q （Q <= 1e5）；

每组测试数据的 2 ~ Q+1 行为具体的操作 （MKDIR、RM 操作总数不超过 5000）；

♔面对数据范围你要思考的是他们代表的 “命令” 执行的最大可接受复杂度，只有这样你才能知道你需要设计的是怎样复杂度的系统。

♔Output

每组测试数据的输出结果间需要输出一行空行。注意大小写敏感。

♔Example

♔Input

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
1
22
MKDIR dira
CD dirb
CD dira
MKDIR a
MKDIR b
MKDIR c
CD ..
MKDIR dirb
CD dirb
MKDIR x
CD ..
MKDIR dirc
CD dirc
MKDIR y
CD ..
SZ
LS
TREE
RM dira
TREE
UNDO
TREE

♔Output

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
OK
ERR
OK
OK
OK
OK
OK
OK
OK
OK
OK
OK
OK
OK
OK
9
dira
dirb
dirc
root
dira
a
b
c
dirb
x
dirc
y
OK
root
dirb
x
dirc
y
OK
root
dira
a
b
c
dirb
x
dirc
y

♔英文原版题面：

img

♔解题思路

这一题还是比较考验码力的，采用一个结构体来表示文件夹的节点，结构体的内容有本文件夹的名字，大小，上一级文件夹的编号以及用map表示的子文件夹的名字与编号的映射。对于创建和删除操作，直接进行即可，同时可以更新本文件夹以及各上层文件夹的大小并在栈中记录本操作。对于UNDO操作，首先查询栈中操作的个数，若无操作则UNDO失败，若有操作则进行栈顶操作的逆操作。对于LS操作，要注意的是输出后五个时用反向迭代器先移动到倒数第五个的位置，然后再向尾部遍历。对于TREE操作，采用懒更新的策略，若当前节点进行TREE操作后其本身及子节点的结构未曾发生变化，则直接输出已经存储过的，否则进行更新。更新时对于后五个节点，采用递归的方式更新，对于每一个遍历到的节点，从后往前遍历其子节点，若子节点的大小大于剩余需要的点数则遍历该节点，否则遍历该节点后将剩余的节点数减去该节点的大小。

♔代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299
300
301
302
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#include<map>
#define ll long long
using namespace std;
struct data
{
	string na;
	int siz,flg,fa;
	string pre[11],bac[11];
	map<string,int> nxt;
}mir[100005];
struct data1
{
	string na;
	int type,zi,snow;
}stck[100005];
int T,n,now,top,ztop,t;
string zl,cs;

void preback(int x,int no)
{
	if(t>10) return;
	mir[x].pre[t++]=mir[no].na;
	//cout<<"++++++"<<mir[no].na<<endl;
	if(mir[no].nxt.size()>0)
	{
		map<string,int>::iterator iter;
		for(iter=mir[no].nxt.begin();iter!=mir[no].nxt.end();iter++)
		{
			preback(x,iter->second);
		}
	}
}

void bacback(int ti,int x,int no)
{
	/*int sz=mir[no].nxt.size();
	map<string,int> ::iterator iter=mir[no].nxt.end();
	while(sz--)
	{
		iter--;
		int szz=mir[iter->second].siz;
		if(szz>=t)
		{
			bacback(ti,x,iter->second);
			return;
		} 
		else
		{
			bacback(szz,x,iter->second);
			ti-=szz;
		}
	}*/
	int ni=ti;
	map<string,int>::reverse_iterator rter;
	for(rter=mir[no].nxt.rbegin();rter!=mir[no].nxt.rend();rter++)
	{
		if(mir[rter->second].siz>=ni)
		{
			bacback(ni,x,rter->second);
			return;
		}
		else 
		{
			bacback(mir[rter->second].siz,x,rter->second);
			ni-=mir[rter->second].siz;
		}
	}
	mir[x].bac[t++]=mir[no].na;
}

void maketree(int x)
{
	t=1;
	mir[x].flg=1;
	//bacback(x,x);
	preback(x,x);
	if(mir[x].siz>10) 
	{
		t=1;
		bacback(5,x,x);
	}
	else 
	{
		for(int i=1;i<=mir[x].siz;i++) 
			mir[x].bac[i]=mir[x].pre[i];
	}
}


void makeupdate(int x,int num)
{
	//cout<<x<<"----"<<num<<endl;
	mir[x].siz+=num;
	mir[x].flg=0;
	if(mir[x].fa) makeupdate(mir[x].fa,num);
}

int main()
{
	//freopen("1.txt","r",stdin);
	//freopen("a1.txt","w",stdout);
	int i,j;
	scanf("%d",&T);
	while(T--)
	{
		for(i=1;i<=99999;i++)
		{
			mir[i].nxt.clear();
			mir[i].flg=0;
			mir[i].siz=0;
		} 
		top=2;now=1;ztop=0;
		//memset(mir,0,sizeof(mir));
		//memset(stck,0,sizeof(stck));
		mir[now].na="root";
		mir[now].flg=1;
		mir[now].siz=1;
		scanf("%d",&n);
		for(i=1;i<=n;i++)
		{
			//cout<<"--"<<mir[now].na<<"--"<<endl;
			cin>>zl;
			if(zl=="MKDIR")
			{
				cin>>cs;
				if(mir[now].nxt.find(cs)!=mir[now].nxt.end())
				{
					printf("ERR\n");
				}
				else
				{
					mir[now].nxt[cs]=top;
					mir[top].na=cs;
					mir[top].fa=now;
					mir[top].siz=0;
					mir[top].flg=0;
					makeupdate(top,1);
					top++;
					stck[++ztop].na=cs;
					stck[ztop].type=1;
					stck[ztop].snow=now;
					printf("OK\n");
				}
			}
			else if(zl=="RM")
			{
				cin>>cs;
				if(mir[now].nxt.find(cs)!=mir[now].nxt.end())
				{
					stck[++ztop].na=cs;
					stck[ztop].type=2;
					stck[ztop].zi=mir[now].nxt[cs];
					stck[ztop].snow=now;
					makeupdate(now,0-(mir[mir[now].nxt[cs]].siz));
					mir[mir[now].nxt[cs]].flg=0;
					mir[now].nxt.erase(cs);
					
					printf("OK\n");
				}
				else
				{
					printf("ERR\n");
				}
			}
			else if(zl=="CD")
			{
				cin>>cs;
				if(cs=="..")
				{
					if(mir[now].fa)
					{
						stck[++ztop].na=mir[now].na;
						stck[ztop].type=3;
						stck[ztop].zi=0;
						stck[ztop].snow=mir[now].fa;
						now=mir[now].fa;
						printf("OK\n");
					}
					else
					{
						printf("ERR\n");
					}
				}
				else if(mir[now].nxt.find(cs)!=mir[now].nxt.end())
				{
					now=mir[now].nxt[cs];
					stck[++ztop].type=3;
					stck[ztop].zi=1;
					stck[ztop].snow=now;
					printf("OK\n");
				}
				else
				{
					printf("ERR\n");
				}
			}
			else if(zl=="SZ")
			{
				printf("%d\n",mir[now].siz);				
			}
			else if(zl=="LS")
			{
				if(mir[now].nxt.size()==0)
				{
					printf("EMPTY\n");
				}
				else if(mir[now].nxt.size()<=10)
				{
					map<string,int>::iterator iter;
					for(iter=mir[now].nxt.begin();iter!=mir[now].nxt.end();iter++)
					{
						cout<<iter->first<<endl;
					}
				}
				else
				{
					map<string,int>::iterator iter;
					for(iter=mir[now].nxt.begin(),j=1;j<=5;j++,iter++)
					{
						cout<<iter->first<<endl;
					}
					cout<<"..."<<endl;
					map<string,int>::reverse_iterator rter;
					for(rter=mir[now].nxt.rbegin(),j=1;j<5;j++,rter++);
					for(j=1;j<=5;j++,rter--)
					{
						cout<<rter->first<<endl;
					}
				}
			}
			else if(zl=="TREE")
			{
				if(!mir[now].flg) maketree(now);
				if(mir[now].nxt.size()==0)
				{
					printf("EMPTY\n");
				}
				else if(mir[now].siz<=10)
				{
					for(j=1;j<=mir[now].siz;j++) cout<<mir[now].pre[j]<<endl;
				}
				else
				{
					for(j=1;j<=5;j++) cout<<mir[now].pre[j]<<endl;
					cout<<"..."<<endl;
					for(j=5;j>=1;j--) cout<<mir[now].bac[j]<<endl;
				}
			}
			else if(zl=="UNDO")
			{
				if(ztop==0)
				{
					printf("ERR\n");
				}
				else
				{
					if(stck[ztop].type==1)
					{
						makeupdate(stck[ztop].snow,0-mir[mir[stck[ztop].snow].nxt[stck[ztop].na]].siz);
						mir[stck[ztop].snow].nxt.erase(stck[ztop].na);
						ztop--;
						printf("OK\n");
					}
					else if(stck[ztop].type==2)
					{
						mir[stck[ztop].snow].nxt[stck[ztop].na]=stck[ztop].zi;
						makeupdate(stck[ztop].snow,mir[stck[ztop].zi].siz);
						ztop--;
						printf("OK\n");
					}
					else if(stck[ztop].type==3)
					{
						if(stck[ztop].zi==0)
						{
							now=mir[stck[ztop].snow].nxt[stck[ztop].na];
							ztop--;
							printf("OK\n");
						}
						else if(stck[ztop].zi==1)
						{
							now=mir[stck[ztop].snow].fa;
							ztop--;
							printf("OK\n");
						}
					}
				}
			}
		}
		if(T) printf("\n");
	}
	return 0;
}

♔B 东东学打牌

♔Problem

最近，东东沉迷于打牌。所以他找到 HRZ、ZJM 等人和他一起打牌。由于人数众多，东东稍微修改了亿下游戏规则：

  • 所有扑克牌只按数字来算大小，忽略花色。
  • 每张扑克牌的大小由一个值表示。A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K 分别指代 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13。
  • 每个玩家抽得 5 张扑克牌，组成一手牌！（每种扑克牌的张数是无限的，你不用担心，东东家里有无数副扑克牌）

理所当然地，一手牌是有不同类型，并且有大小之分的。

举个栗子，现在东东的 “一手牌”（记为 α），瑞神的 “一手牌”（记为 β），要么 α > β，要么 α < β，要么 α = β。

那么这两个 “一手牌”，如何进行比较大小呢？首先对于不同类型的一手牌，其值的大小即下面的标号；对于同类型的一手牌，根据组成这手牌的 5 张牌不同，其值不同。下面依次列举了这手牌的形成规则：

  1. 大牌：这手牌不符合下面任一个形成规则。如果 α 和 β 都是大牌，那么定义它们的大小为组成这手牌的 5 张牌的大小总和。
  2. 对子：5 张牌中有 2 张牌的值相等。如果 α 和 β 都是对子，比较这个 “对子” 的大小，如果 α 和 β 的 “对子” 大小相等，那么比较剩下 3 张牌的总和。
  3. 两对：5 张牌中有两个不同的对子。如果 α 和 β 都是两对，先比较双方较大的那个对子，如果相等，再比较双方较小的那个对子，如果还相等，只能比较 5 张牌中的最后那张牌组不成对子的牌。
  4. 三个：5 张牌中有 3 张牌的值相等。如果 α 和 β 都是 “三个”，比较这个 “三个” 的大小，如果 α 和 β 的 “三个” 大小相等，那么比较剩下 2 张牌的总和。
  5. 三带二：5 张牌中有 3 张牌的值相等，另外 2 张牌值也相等。如果 α 和 β 都是 “三带二”，先比较它们的 “三个” 的大小，如果相等，再比较 “对子” 的大小。
  6. 炸弹：5 张牌中有 4 张牌的值相等。如果 α 和 β 都是 “炸弹”，比较 “炸弹” 的大小，如果相等，比较剩下那张牌的大小。
  7. 顺子：5 张牌中形成 x, x+1, x+2, x+3, x+4。如果 α 和 β 都是 “顺子”，直接比较两个顺子的最大值。
  8. 龙顺：5 张牌分别为 10、J、Q、K、A。

作为一个称职的魔法师，东东得知了全场人手里 5 张牌的情况。他现在要输出一个排行榜。排行榜按照选手们的 “一手牌” 大小进行排序，如果两个选手的牌相等，那么人名字典序小的排在前面。

不料，此时一束宇宙射线扫过，为了躲避宇宙射线，东东慌乱中清空了他脑中的 Cache。请你告诉东东，全场人的排名。

♔Input

输入包含多组数据。每组输入开头一个整数 n (1 <= n <= 1e5)，表明全场共多少人。
随后是 n 行，每行一个字符串 s1 和 s2 （1 <= |s1|,|s2| <= 10）， s1 是对应人的名字，s2 是他手里的牌情况。

♔Output

对于每组测试数据，输出 n 行，即这次全场人的排名。

♔Examples

♔Input

1
2
3
4
3
DongDong AAA109
ZJM 678910
Hrz 678910

♔Output

1
2
3
Hrz
ZJM
DongDong

♔解题思路

这一题和上一次的打牌那个题比较像，对于每一个玩家，判断其手牌的类型，并提取关键字及关键字个数，和玩家名一起存储到结构体中。并用自定义了比较函数的sort函数对该结构体进行排序，然后按顺序输出玩家名称即可。

♔代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#define ll long long
using namespace std;
struct data
{
	int typ,flgs,flg[4];
	string na;
}pl[100005];
int n;
string c;

void gettyp(int x)
{
	int pi[5];
	int cnt=0;
	int len=c.length();
	for(int i=0;i<len;i++)
	{
		if(c[i]=='1') 
		{
			pi[cnt++]=10;
			i++;
		}
		else if(c[i]>='2' && c[i]<='9')
			pi[cnt++]=c[i]-'0';
		else if(c[i]=='A')
			pi[cnt++]=1;
		else if(c[i]=='J')
			pi[cnt++]=11;
		else if(c[i]=='Q')
			pi[cnt++]=12;
		else if(c[i]=='K')
			pi[cnt++]=13;
	}
	sort(pi,pi+5);
	/*if(pi[0]==pi[1] && pi[1]==pi[2] && pi[2]==pi[3] && pi[3]==pi[4])
	{
		pl[x].typ=1;
		pl[x].flg[1]=pi[0]+pi[1]+pi[2]+pi[3]+pi[4];
		pl[x].flgs=1;
	}
	else*/ if(pi[0]==1 && pi[1]==10 && pi[2]==11 && pi[3]==12 && pi[4]==13)//longshun 
	{
		pl[x].typ=8;
		pl[x].flgs=0;
	}	
	else if(pi[0]+1==pi[1] && pi[1]+1==pi[2] && pi[2]+1==pi[3] && pi[3]+1==pi[4])//shunzi
	{
		pl[x].typ=7;
		pl[x].flg[1]=pi[4];
		pl[x].flgs=1;
	}
	else if(pi[0]==pi[1] && pi[1]==pi[2] && pi[2]==pi[3])//0123 4
	{
		pl[x].typ=6;
		pl[x].flg[1]=pi[0];
		pl[x].flg[2]=pi[4];
		pl[x].flgs=2;
	}
	else if(pi[1]==pi[2] && pi[2]==pi[3] && pi[3]==pi[4])//0 1234
	{
		pl[x].typ=6;
		pl[x].flg[1]=pi[4];
		pl[x].flg[2]=pi[0];
		pl[x].flgs=2;
	}
	else if(pi[0]==pi[1] && pi[1]==pi[2])//012 3 4
	{
		if(pi[3]==pi[4])
		{
			pl[x].typ=5;
			pl[x].flg[1]=pi[0];
			pl[x].flg[2]=pi[3];
			pl[x].flgs=2;
		}
		else
		{
			pl[x].typ=4;
			pl[x].flg[1]=pi[0];
			pl[x].flg[2]=pi[3]+pi[4];
			pl[x].flgs=2;
		}
	}
	else if(pi[2]==pi[3] && pi[3]==pi[4])//0 1 234
	{
		if(pi[0]==pi[1])
		{
			pl[x].typ=5;
			pl[x].flg[1]=pi[4];
			pl[x].flg[2]=pi[0];
			pl[x].flgs=2;
		}
		else
		{
			pl[x].typ=4;
			pl[x].flg[1]=pi[4];
			pl[x].flg[2]=pi[0]+pi[1];
			pl[x].flgs=2;
		}
	}
	else if(pi[1]==pi[2] && pi[2]==pi[3])//0 123 4
	{
		pl[x].typ=4;
		pl[x].flg[1]=pi[1];
		pl[x].flg[2]=pi[0]+pi[4];
		pl[x].flgs=2;
	}
	else if(pi[0]==pi[1] && pi[2]==pi[3])//01 23 4
	{
		pl[x].typ=3;
		pl[x].flg[1]=pi[3];
		pl[x].flg[2]=pi[1];
		pl[x].flg[3]=pi[4];
		pl[x].flgs=3;
	}
	else if(pi[0]==pi[1] && pi[3]==pi[4])//01 2 34
	{
		pl[x].typ=3;
		pl[x].flg[1]=pi[4];
		pl[x].flg[2]=pi[1];
		pl[x].flg[3]=pi[2];
		pl[x].flgs=3;
	}
	else if(pi[1]==pi[2] && pi[3]==pi[4])//0 12 34
	{
		pl[x].typ=3;
		pl[x].flg[1]=pi[4];
		pl[x].flg[2]=pi[1];
		pl[x].flg[3]=pi[0];
		pl[x].flgs=3;
	}
	else if(pi[0]==pi[1])//01 2 3 4
	{
		pl[x].typ=2;
		pl[x].flg[1]=pi[0];
		pl[x].flg[2]=pi[2]+pi[3]+pi[4];
		pl[x].flgs=2;
	}
	else if(pi[1]==pi[2])//0 12 3 4
	{
		pl[x].typ=2;
		pl[x].flg[1]=pi[1];
		pl[x].flg[2]=pi[0]+pi[3]+pi[4];
		pl[x].flgs=2;
	}
	else if(pi[2]==pi[3])//0 1 23 4
	{
		pl[x].typ=2;
		pl[x].flg[1]=pi[2];
		pl[x].flg[2]=pi[0]+pi[1]+pi[4];
		pl[x].flgs=2;
	}
	else if(pi[3]==pi[4])//0 1 2 34
	{
		pl[x].typ=2;
		pl[x].flg[1]=pi[3];
		pl[x].flg[2]=pi[0]+pi[1]+pi[2];
		pl[x].flgs=2;
	}
	else
	{
		pl[x].typ=1;
		pl[x].flg[1]=pi[0]+pi[1]+pi[2]+pi[3]+pi[4];
		pl[x].flgs=1;
	}
}

int wly(data x,data y)
{
	if(x.typ!=y.typ) return x.typ>y.typ;
	if(x.typ==y.typ)
	{
		for(int i=1;i<=x.flgs;i++)
		{
			if(x.flg[i]!=y.flg[i]) return x.flg[i]>y.flg[i];
		}
		return x.na<y.na;
	}
	//return 0;
}

int main()
{
	
	int i,j;
	while(scanf("%d",&n)!=EOF)
	{
		for(i=1;i<=n;i++)
		{
			cin>>pl[i].na>>c;
			gettyp(i);
		}
		sort(pl+1,pl+1+n,wly);
		for(i=1;i<=n;i++)
		{
			//printf("-%d %d %d %d %d-\n",pl[i].typ,pl[i].flg[1],pl[i].flg[2],pl[i].flg[3],pl[i].flgs);
			printf("%s\n",pl[i].na.c_str());
		}
	}
	return 0;
}

♔C 签到题

♔Problem

公园有 x 条长凳。第 i 个长凳上坐着 a_i 个人。这时候又有 y 个人将来到公园，他们将选择坐在某些公园中的长凳上，那么当这 y 个人坐下后，记k = 所有椅子上的人数的最大值，那么k可能的最大值mx和最小值mn分别是多少。

♔Input

第一行包含一个整数 x (1 <= x <= 100) 表示公园中长椅的数目
第二行包含一个整数 y (1 <= y <= 1000) 表示有 y 个人来到公园
接下来 x 个整数 a_i (1<=a_i<=100)，表示初始时公园长椅上坐着的人数

♔Output

输出 mn 和 mx

♔Examples

♔Input

1
2
3
4
5
3
7
1
6
1

♔Output

1
6 13

♔解题思路

这一题比较简单，对于最大值最大，直接输出最大值加新来的人数即可；对于最大值最小先求出各个椅子上最大的人数，然后求出各椅子上人数与最大人数的差的和，若和大于等于新来的人数，则直接输出最大值，否则输出（最大值-新来的人数）/ 椅子数的上取整结果。

♔代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#define ll long long
using namespace std;
int n,m,maxn,ksum;
int a[105]; 

int main()
{
	int i,j,k;
	scanf("%d",&n);
	scanf("%d",&m);
	for(i=1;i<=n;i++)
	{
		scanf("%d",&a[i]);
		maxn=max(maxn,a[i]);
	}
	for(i=1;i<=n;i++) ksum+=(maxn-a[i]);
	if(ksum>=m) printf("%d",maxn);
	else
	{
		printf("%d",maxn+(m-ksum+n-1)/n);
	}
	printf(" %d",maxn+m);
	return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！