【作业向】程序设计思维与实践 Week5 作业

发表于 | 分类于 ，
字数统计: 2.3k | 阅读时长 ≈ 11

【作业向】程序设计思维与实践 Week5 作业

♔A 最大矩形

♔Problem

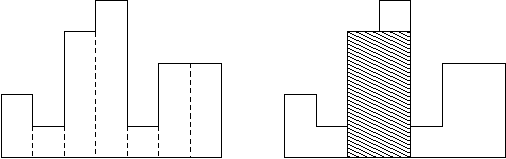
给一个直方图，求直方图中的最大矩形的面积。例如，下面这个图片中直方图的高度从左到右分别是2, 1, 4, 5, 1, 3, 3, 他们的宽都是1，其中最大的矩形是阴影部分。

img

♔Input

输入包含多组数据。每组数据用一个整数n来表示直方图中小矩形的个数，你可以假定1 <= n <= 100000. 然后接下来n个整数h1, …, hn, 满足 0 <= hi <= 1000000000. 这些数字表示直方图中从左到右每个小矩形的高度，每个小矩形的宽度为1。 测试数据以0结尾。

♔Output

对于每组测试数据输出一行一个整数表示答案。

♔Example

♔Input

1
2
3
7 2 1 4 5 1 3 3
4 1000 1000 1000 1000
0

♔Output

1
2
8
4000

♔解题思路

一道单调栈的题目，定义结构体类型data用来在栈中存储每个矩形的高度和位置。对于第i个矩形，若i的高度大于栈顶元素的高度，则直接将其放入栈中，否则计算栈顶元素的高度h可构成的最大面积，最大面积为h×（i-1-栈顶元素下面那个元素的座标），并以此来更新答案。继续循环，直到栈顶元素的高度小于i的高度，将i放入栈中。当所有元素处理完成之后，按顺序将栈中的元素弹出，并计算其面积用来更新答案，直到栈空为止。最后输出面积的最大值即可。

♔代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#define ll long long
using namespace std;
struct data 
{
	ll h,index;
}stac[100005];
ll n,maxs,top;

int main()
{
	ll i,j;
	data t;
	scanf("%lld",&n);
	while(n)
	{
		maxs=0;
		top=0;
		scanf("%lld",&t.h);
		t.index=1;
		stac[++top]=t;
		for(i=2;i<=n;i++)
		{
			scanf("%lld",&t.h);
			if(t.h>=stac[top].h)
			{
				t.index=i;
				stac[++top]=t;
			}
			else
			{
				while(t.h<stac[top].h && top)
				{
					if(top>1) maxs=max(maxs,stac[top].h*(i-stac[top-1].index-1));
					else maxs=max(maxs,stac[top].h*(i-1));
					top--;
				} 
				t.index=i;
				stac[++top]=t;
			}		
		}
		while(top)
		{
			if(top>1) maxs=max(maxs,stac[top].h*(n-stac[top-1].index));
			else maxs=max(maxs,stac[top].h*(n));
			top--;
		}
		printf("%lld\n",maxs);
		scanf("%lld",&n);
	}
	return 0;
}

♔B TT’s Magic Cat

♔Problem

Thanks to everyone’s help last week, TT finally got a cute cat. But what TT didn’t expect is that this is a magic cat.

One day, the magic cat decided to investigate TT’s ability by giving a problem to him. That is select nn cities from the world map, and a[i]a[i] represents the asset value owned by the ii-th city.

Then the magic cat will perform several operations. Each turn is to choose the city in the interval [l,r][l,r] and increase their asset value by cc. And finally, it is required to give the asset value of each city after qq operations.

Could you help TT find the answer?

♔Input

The first line contains two integers n,q (1≤n,q≤2⋅1e5) — the number of cities and operations.

The second line contains elements of the sequence a: integer numbers a1,a2,…,an(−1e6≤ai≤1e6).

Then qq lines follow, each line represents an operation. The i-th line contains three integers l,r and c (1≤l≤r≤n,−1e5≤c≤1e5)for the i-th operation.

♔Output

Print nn integers a1,a2,…,an one per line, and aiai should be equal to the final asset value of the i-th city.

♔Examples

♔Input

1
2
3
4
4 2
-3 6 8 4
4 4 -2
3 3 1

♔Output

1
-3 6 9 2

♔解题思路

这一题用前缀和求解即可，对于每一次更改，在标记数组b中b[l]+=c,b[r+1]-=c。然后对b数组求前缀和，最后依次输出a[i]+b[i]即可。

♔代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#define ll long long
using namespace std;
ll n,q,l,r,a[200005],b[200005];


int main()
{
	ll i,j;
	scanf("%lld%lld",&n,&q);
	for(i=1;i<=n;i++) scanf("%lld",&a[i]);
	for(i=1;i<=q;i++)
	{
		scanf("%lld%lld%lld",&l,&r,&j);
		b[l]+=j,b[r+1]-=j;
	}
	for(i=1;i<=n;i++)
	{
		b[i]+=b[i-1];
		printf("%lld ",a[i]+b[i]);
	}
	return 0;
}

♔C 平衡字符串

♔Problem

一个长度为 n 的字符串 s，其中仅包含 ‘Q’, ‘W’, ‘E’, ‘R’ 四种字符。

如果四种字符在字符串中出现次数均为 n/4，则其为一个平衡字符串。

现可以将 s 中连续的一段子串替换成相同长度的只包含那四个字符的任意字符串，使其变为一个平衡字符串，问替换子串的最小长度?

如果 s 已经平衡则输出0。

♔Input

一行字符表示给定的字符串s

♔Output

一个整数表示答案

♔Examples

♔Input

1
QQER

♔Output

1
1

♔解题思路

使用尺取法来解这道题，设定两个标记f1，f2。计算区间f1，f2之外的各个字母的数量sum1~4 ,取maxs=max(sum1~4)，且tot=(f2-f1)-∑（maxs-sumi）。若tot大于等于0且为4的整数倍，则当前区间可以使字符串合法，用当前区间的长度更新答案，f1++；否则f2++。处理结束之后输出最小的区间长度即可。

♔代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#define ll long long
using namespace std;
int n,f1,f2,sum[5],minx=0x7fffffff;
char a[100005];

int main()
{
	int i,j,maxi,tot;
	scanf("%s",a);
	n=strlen(a);
	for(i=1;i<n;i++)
	{
		if(a[i]=='Q') sum[1]++;
		else if(a[i]=='W') sum[2]++;
		else if(a[i]=='E') sum[3]++;
		else if(a[i]=='R') sum[4]++;
	}
	f1=0;
	f2=-1;
	while(f1<n && f2<n)
	{
		maxi=max(sum[1],sum[2]);
		maxi=max(maxi,sum[3]);
		maxi=max(maxi,sum[4]);
		tot=f1-f2;
		for(i=1;i<=4;i++)
			tot=tot-(maxi-sum[i]);//,printf("%d ",sum[i])
		//printf(" %d %d %d--\n",f1,f2,tot);
		if(tot>=0 && tot%4==0)
		{
			minx=min(minx,f1-f2);
			f2++;
			if(a[f2]=='Q') sum[1]++;
			else if(a[f2]=='W') sum[2]++;
			else if(a[f2]=='E') sum[3]++;
			else if(a[f2]=='R') sum[4]++;
		}
		else 
		{
			f1++;
			if(a[f1]=='Q') sum[1]--;
			else if(a[f1]=='W') sum[2]--;
			else if(a[f1]=='E') sum[3]--;
			else if(a[f1]=='R') sum[4]--;
		}		
	}
	printf("%d",minx);
	return 0;
}

♔D 滑动窗口

♔Problem

ZJM 有一个长度为 n 的数列和一个大小为 k 的窗口, 窗口可以在数列上来回移动. 现在 ZJM 想知道在窗口从左往右滑的时候，每次窗口内数的最大值和最小值分别是多少. 例如：
数列是 [1 3 -1 -3 5 3 6 7], 其中 k 等于 3.

Window position Minimum value Maximum value
[1 3 -1] -3 5 3 6 7 -1 3
1 [3 -1 -3] 5 3 6 7 -3 3
1 3 [-1 -3 5] 3 6 7 -3 5
1 3 -1 [-3 5 3] 6 7 -3 5
1 3 -1 -3 [5 3 6] 7 3 6
1 3 -1 -3 5 [3 6 7] 3 7

♔Input

输入有两行。第一行两个整数n和k分别表示数列的长度和滑动窗口的大小，1<=k<=n<=1000000。第二行有n个整数表示ZJM的数列。

♔Output

输出有两行。第一行输出滑动窗口在从左到右的每个位置时，滑动窗口中的最小值。第二行是最大值。

♔Examples

♔Input

1
2
8 3
1 3 -1 -3 5 3 6 7

♔Output

1
2
-1 -3 -3 -3 3 3
3 3 5 5 6 7

♔解题思路

我们用单调队列来解这道题，依旧定义结构体类型data来在栈中存储元素的数值即下标。对于取最小值，我们需要一个单调不减的队列对于第i个元素，我们需要从队尾开始判断，若第i个元素小于队尾元素，则将队尾元素弹出，直到第i个元素大于等于队尾元素再将第i个元素加入队列。同时对于每一次窗口的滑动，我们还要判断队列中的元素是否过时。因为队列中的元素加入队列的时间是严格递增的，故我们从队列头部开始判断，若队首元素的下标小于等于i-k，则队首元素出队，直到队首元素大于i-k为止。此时，队首元素即为当前窗口内的最小元素。

求最大元素的过程与上面类似，只不过是改为使用单调不增的队列。

♔代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#define ll long long
using namespace std;
struct data
{
	int x,i;
}q[1000005];
int n,k,head,tail;
int a[1000005];

int main()
{
	int i,j;
	scanf("%d%d",&n,&k);
	for(i=1;i<=n;i++) scanf("%d",&a[i]);
	for(i=1;i<=n;i++)
	{
		while(tail>head && a[i]<q[tail-1].x) tail--;
		q[tail].x=a[i],q[tail].i=i;
		tail++;
		while(head<tail && q[head].i<=i-k) head++;
		if(i>=k) printf("%d ",q[head].x);
	}
	printf("\n");
	head=0,tail=0;
	for(i=1;i<=n;i++)
	{
		while(tail>head && a[i]>q[tail-1].x) tail--;
		q[tail].x=a[i],q[tail].i=i;
		tail++;
		while(head<tail && q[head].i<=i-k) head++;
		if(i>=k) printf("%d ",q[head].x);
	}
	return 0;
}
坚持原创技术分享，您的支持将鼓励我继续创作！