CCF CSP 201512-4 送货

♔问题描述

为了增加公司收入，F公司新开设了物流业务。由于F公司在业界的良好口碑，物流业务一开通即受到了消费者的欢迎，物流业务马上遍及了城市的每条街道。然而，F公司现在只安排了小明一个人负责所有街道的服务。
　　任务虽然繁重，但是小明有足够的信心，他拿到了城市的地图，准备研究最好的方案。城市中有n个交叉路口，m条街道连接在这些交叉路口之间，每条街道的首尾都正好连接着一个交叉路口。除开街道的首尾端点，街道不会在其他位置与其他街道相交。每个交叉路口都至少连接着一条街道，有的交叉路口可能只连接着一条或两条街道。
　　小明希望设计一个方案，从编号为1的交叉路口出发，每次必须沿街道去往街道另一端的路口，再从新的路口出发去往下一个路口，直到所有的街道都经过了正好一次。

♔输入格式

输入的第一行包含两个整数n, m，表示交叉路口的数量和街道的数量，交叉路口从1到n标号。
　　接下来m行，每行两个整数a, b，表示和标号为a的交叉路口和标号为b的交叉路口之间有一条街道，街道是双向的，小明可以从任意一端走向另一端。两个路口之间最多有一条街道。

♔输出格式

如果小明可以经过每条街道正好一次，则输出一行包含m+1个整数p1, p2, p3, …, pm+1，表示小明经过的路口的顺序，相邻两个整数之间用一个空格分隔。如果有多种方案满足条件，则输出字典序最小的一种方案，即首先保证p1最小，p1最小的前提下再保证p2最小，依此类推。
　　如果不存在方案使得小明经过每条街道正好一次，则输出一个整数-1。

♔样例输入

4 5
1 2
1 3
1 4
2 4
3 4

♔样例输出

1 2 4 1 3 4

♔样例说明

城市的地图和小明的路径如下图所示。

♔样例输入

4 6
1 2
1 3
1 4
2 4
3 4
2 3

♔样例输出

-1

♔样例说明

城市的地图如下图所示，不存在满足条件的路径。

♔评测用例规模与约定

前30%的评测用例满足：1 ≤ n ≤ 10, n-1 ≤ m ≤ 20。
　　前50%的评测用例满足：1 ≤ n ≤ 100, n-1 ≤ m ≤ 10000。
　　所有评测用例满足：1 ≤ n ≤ 10000，n-1 ≤ m ≤ 100000。

♔解题思路

​ 根据题意可知，这一题要首先要判断图是否联通，然后再判断图中是否存在欧拉路径或欧拉回路，即要么图中只有两个度数为奇数的点且编号为1的顶点的度数为奇数，要么没有度数为奇数的点。确定好之后通过dfs寻找路径即可。需要注意的是直接搜索的话会爆栈，只能得80分，那么我们就需要用手工栈来模拟dfs，这样就可以a掉了。

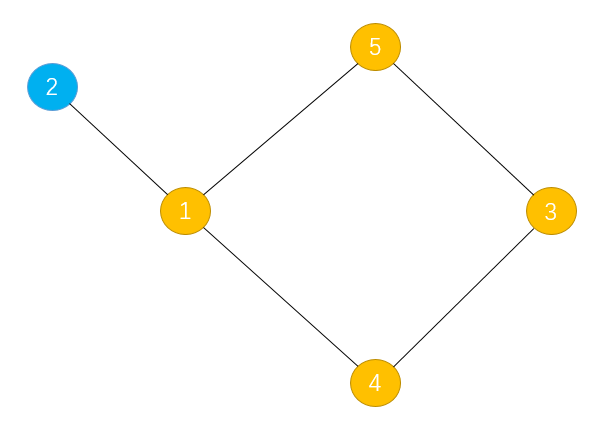
​ 以及，根据这个博客所说，我们需要在递归回来之后才将该节点添加入栈，相当于倒序储存。一般情况下和用队列顺序存储差别不大。但是有一种存在孤点的图。如下图所示：

图中点2 是孤立点，如果每次搜索到一个节点就存储进队列的话，就会出现错误，而用栈倒序存储就能解决这个问题。

♔代码

#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<iostream>
#include<algorithm>
#include<cmath>
#include<queue>
#include<stack>
#include<vector>
#include<utility>
#include<sstream>
#define ll long long
using namespace std;
int n,m;
int lu[1000005],d[100005];
bool tu[10005][10005],visit[100005];
vector<int> po[100005];
int dsum,s1,s2;
stack<int> st;

void dfs(int x)
{
	int i;
//	if(dsum==m+1)
//	{
//		for(i=1;i<=dsum;i++)
//			printf("%d ",lu[i]);
//		exit(0);
//	}
	for(i=0;i<po[x].size();i++)
	{
		if(tu[x][po[x][i]])
		{
			
			tu[x][po[x][i]]=0;
			tu[po[x][i]][x]=0;
			dfs(po[x][i]);
			//tu[x][po[x][i]]=1;
			//tu[po[x][i]][x]=1;
			//dsum--;
		}
	}
	lu[++dsum]=x;
}

void make(int x)
{
	int i;
	for(i=0;i<po[x].size();i++)
	{
		if(!visit[po[x][i]])
		{
			visit[po[x][i]]=1;
			make(po[x][i]);
		}
	}
}

int main()
{
	int i,j,k;
	scanf("%d%d",&n,&m);
	for(i=1;i<=m;i++)
	{
		scanf("%d%d",&j,&k);
		tu[j][k]=1;
		tu[k][j]=1;
		po[j].push_back(k);
		po[k].push_back(j);
		d[j]++,d[k]++;
	}
	for(i=1;i<=n;i++)
	{
		sort(po[i].begin(),po[i].end());
		if(d[i]%2)
		{
			if(dsum==2)
			{
				printf("-1");
				return 0;
			}
			if(!dsum)
				s1=i;
			else 
				s2=i;
			dsum++;
		}
	}
	if(dsum==1)
	{
		printf("-1");
		return 0;
	}
	if(!dsum) s1=s2=1;
	if(dsum==2)
	{
		if(s1>s2) swap(s1,s2); 
		if(s1!=1)
		{
			printf("-1");
			return 0;
		}
	} 
	visit[1]=1;
	make(1);
	for(i=1;i<=n;i++)
	{
		if(!visit[i])
		{
			printf("-1");
			return 0;
		}
	}
	dsum=0;
	//lu[dsum]=s1;
	//dfs(s1);
	st.push(1);
	while(!st.empty())
	{
		int x=st.top();
		int flag=0;
		for(i=0;i<po[x].size();i++)
		{
			if(tu[x][po[x][i]])
			{
				tu[x][po[x][i]]=0;
				tu[po[x][i]][x]=0;
				st.push(po[x][i]);
				flag=1;
				break;
			}
		}
		if(flag==0) lu[++dsum]=x,st.pop();
	}
	for(i=dsum;i>=1;i--)
		printf("%d ",lu[i]);
	return 0;
}